Starkfeldphysik in Graphen

Ultraschnelle Kontrolle über Ströme in Graphen

„Wie schnell kann man einen Strom einschalten?“ Das ist eine fundamental wichtige Frage, um die Geschwindigkeit moderner Elektronik zu erhöhen. Dies ist wichtig, da Informationen und Signale mittels Elektronenströme übertragen werden. Gemeinsam mit der Gruppe von Prof. Dr. Heiko B. Weber, Lehrstuhl für Angewandte Physik der FAU, präsentieren wir ein neuartiges Konzept, das es ermöglicht, Ströme in Graphen, einem exotischen, leitfähigen Material, ultraschnell auf der Zeitskala einer einzigen Femtosekunde einzuschalten (1 Femtosekunde ist ein Milliardstel einer millionstel Sekunde) [1].

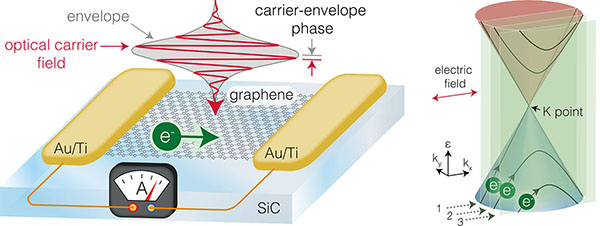
Schematischer Messaufbau zur Bestimmung Lichtfeld-abhängigen Stroms in Graphen (links). Graphens charakteristische doppelkegelförmige Dirac-Dispersionsrelation ermöglicht es uns, Elektronen besonders einfach mit vergleichsweise schwachen optischen Feldern im Starkfeldregime zu lenken. Dabei wird deren Dynamik durch eine Kombination von Band-Band Übergängen und Beschleunigungen in einem einzelnen Band beschrieben (rechts).

Wenn Lichtdetektoren wie in Digitalkameras oder Solarzellen mit Licht beleuchtet werden, werden Elektronen in diesen Materialien vom Valenzband in das Leitungsband angeregt, was zur Erzeugung von Photoströmen führt. Die Zeitskala dieser Prozesse ist üblicherweise durch die Dauer des Laserpulses limitiert, da die Lichtabsorption über die gesamte Pulsdauer erfolgt. Wenn jedoch sehr intensive Laserpulse verwendet werden, kann eine signifikante Anregung innerhalb eines Bruchteils eines einzigen optischen Zyklus auftreten. In der Regel besteht ein Laserpuls aus Dutzenden bis Hunderten oder Tausenden von optischen Zyklen. In unserem Fall haben wir mit extrem kurzen optischen Impulsen gearbeitet, die aus nur zwei Zyklen bestehen. Diese kurze Pulsdauer und die große Feldstärke erlaubten es uns, einen Übergang zum sogenannten Starkfeldregime zu beobachten, der auftritt, wenn die Stärke der Licht-Materie-Wechselwirkung die Photonenenergie übertrifft [2].

Eine solche lichtfeldgetriebene Anregung wurde bereits in gasförmigen Medien [3] und Dielektrika nachgewiesen [4], aber bisher nicht in leitfähigen Materialien. Eine Herausforderung in dieser Materialklasse liegt darin, dass gewöhnliche Metalle Licht reflektieren und somit starke optische Felder nicht auf die Elektronen innerhalb der Metallen wirken können. Graphen, eine atomar dünne Schicht von Kohlenstoffatomen, erlaubt uns, diese Schwierigkeit zu überwinden – es ist so dünn, dass das Licht direkt auf Elektronen in Graphen wirken kann, während das Licht das Material durchdringt [5].

Experimenteller Aufbau um die Femtosekundenpulse auf die evakuierte Probe zu fokussieren (links). Siliziumkarbid-Substrat mit Graphenstrukturen und Goldkontakten (rechts).

Wir testen die Möglichkeit, Ströme in Graphen mit einem lichtfeldgetriebenen Prozess zu kontrollieren, indem wir Graphen mit Laserpulsen weniger Zyklen, linearer Polarisation und einer kontrollierten Träger-Einhüllenden Phase (TEP) beleuchten. Die TEP ist ein Schlüsselparameter zur Beschreibung der Form des elektrischen Feldes eines Laserpulses. Wir haben festgestellt, dass der Strom, der in Graphen erzeugt wird, empfindlich auf die TEP reagiert. Darüber hinaus ändert dieser Strom seine Richtung, wenn man die Laserintensität erhöht. Die Feldstärke von 2 V/nm, bei der diese auffällige Stromrichtungsumkehr stattfindet, entspricht unserer theoretischen Vorhersage und unterstreicht, dass der Elektronenanregungsprozess in das Starkfeldregime übergeht.

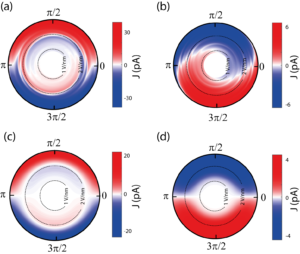
(a) Gemessener CEP-abhängiger Strom unter Verwendung von linear polarisiertem Licht. In diesen Polarplots entspricht der Radius der maximalen elektrischen Feldstärke E, die von 0,5 V/nm bis 3 V/nm variiert, während der Polarwinkel die Träger-Einhüllen Phase darstellt. Die Farbkodierung stellt den CEP-abhängigen Strom dar, gemessen in einem Lock-in-Verfahren. (b) Polardiagramm für zirkular polarisiertes Licht. (c),(d) Numerische Simulation des Stroms für linear bzw. zirkular polarisiertes Licht. Alle wesentlichen Charakteristika der experimentellen Daten werden quantitativ reproduziert.

Darüber hinaus haben wir herausgefunden, dass dort die Elektronendynamik als wiederholte Landau-Zener-Übergänge beschrieben werden kann [6], [7]: Im reziproken Raum ändert sich der Impuls eines Elektrons aufgrund seiner Beschleunigung durch das optische Feld. Wenn das Elektron in die Nähe des Dirac-Punktes der Graphen-Bandstruktur kommt, an der sich Leitungs- und Valenzband berühren, wird die Wellenfunktion des Elektrons kohärent in die Überlagerung der beiden Bandzustände aufgeteilt. Nach einem halben optischen Zyklus treffen sich diese Anteile der Elektronenwellenfunktionen wieder, und je nach Phasenbeziehung zwischen ihnen werden Elektronen weiter zum Leitungsband angeregt oder kehren zum Valenzband zurück. Die Interferenz, kontrolliert durch die TEP des Laserpulses, ist auch bekannt als Landau-Zener-Stückelberg-Interferenz (LZS-Interferenz) und bestimmt somit die Richtung des Stroms [8], [9]. Darüber hinaus können wir die LZS-Interferenz über den Polarisationszustand des Lichts ein- und ausschalten. Mit zirkular polarisiertem Licht ändert sich der Strom nicht als Funktion der Laserintensität, was ebenfalls durch unsere numerischen Simulationen unterstützt wird.

Die nächste Generation von lichtfeldangetriebenen Transistoren

Wenn ein zweiter Laserpuls, senkrecht zum ersten Puls polarisiert, auf Graphen geschickt wird, können die Quantenwege zweidimensional gesteuert werden (siehe Abbildung) [10]. Abhängig von der genauen Form der beiden Wellenformen und der zeitlichen Verzögerung beider Pulse ist es möglich, die Quanten-Interferenz ein- und auszuschalten und damit die Stromrichtung zu steuern. Bemerkenswert ist, dass in diesem Prozess die Kohärenz der Elektronen erhalten bleibt, d.h. das Elektron behält seine Wellencharakteristik während der Licht-Materie-Wechselwirkung bei, auch bei Raumtemperatur.

(a) Gemessener TEP-abhängiger Strom als Funktion der zeitlichen Verzögerung zwischen zwei orthogonal polarisierten gepulsten Laserpulsen. Im rot hinterlegten Bereich ist der Strom positiv und zeigt das LZS-Regime an, während im grün gefärbten Bereich der Strom negativ ist und LZS ausgeschaltet ist. Die Simulation ist als orange gestrichelte Linie dargestellt. Bei geblockten Kontrollpulsen ist die Stromamplitude positiv, während bei geblockten Treiberpulsen kein messbarer CEP-abhängiger Strom aufgezeichnet wird (rechte Abbildung). (b) Der jeweilige Hauptpolarisationszustand (hier vereinfacht für einen einzigen optischen Zyklus) wird für unterschiedliche Verzögerungen zwischen Kontroll- und Treiberpuls dargestellt.

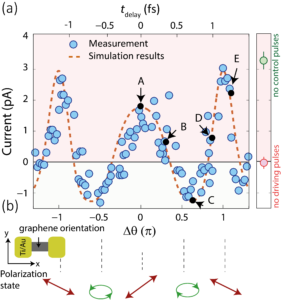
Unsere Ergebnisse sind sowohl für die Grundlagenforschung als auch für zukünftige Anwendungen interessant, da sie es ermöglichen, Prozesse zu untersuchen, die auf extrem kurzen Zeitskalen ablaufen. Dazu gehört beispielsweise die Frage, wie lange es dauert, bis ein Elektron die Anwesenheit anderer Elektronen wahrnimmt. Eine Anwendung, wie vorstehend erläutert, könnte die Elektronik sein, da es möglich sein wird, Ströme mit einer Petahertz Frequenzen zu steuern, die in zukünftiger Elektronik eingesetzt werden könnten. Diese Ergebnisse stellen einen wichtigen Schritt dar, um zwei wichtige Bereiche der modernen Technologien, Elektronik und Optik, auf einer einzigen Plattform zusammenzuführen.

Die Form zweier TEP-stabiler Laserpulse (rote und grüne Wellenform) kann die Symmetrie brechen und einen elektrischen Strom in einer ansonsten vollständig symmetrischen Graphenstruktur induzieren. Abhängig vom gemeinsamen Polarisationszustand beider Lichtfelder fließt der feldgetriebene Strom im Graphen in die eine oder andere Richtung. Dies stellt einen bipolaren optischen Feldeffekttransistor dar, bei dem das Vorhandensein des Feldes in senkrechter Richtung die Stromrichtung ändert, ohne selbst einen Strom zu erzeugen.

[1] T. Higuchi, C. Heide, K. Ullmann, H. B. Weber, and P. Hommelhoff, “Light-field-driven currents in graphene,” Nature, 550, 7675 (2017).

[2] C. Heide, T. Boolakee, T. Higuchi, H. B. Weber, and P. Hommelhoff, “Interaction of carrier envelope phase-stable laser pulses with graphene: the transition from the weak-field to the strong-field regime,” New J. Phys., 21, 4 (2019).

[3] P. B. Corkum and F. Krausz, “Attosecond science,” Nat. Phys., 3, 6 (2007).

[4] A. Schiffrin et al., “Optical-field-induced current in dielectrics,” Nature, 493, 7430 (2012).

[5] A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, “The electronic properties of graphene,” Rev. Mod. Phys., 81, 1, (2009).

[6] L. D. Landau, “Zur Theorie der Energieubertragung II,” Z. Sowjetunion, 2, 46–51 (1932).

[7] C. Zener, “Non-Adiabatic Crossing of Energy Levels,” Proc. R. Soc. A Math. Phys. Eng. Sci., 137, 833, (1932).

[8] E. C. G. Stückelberg, “Two-level strong binding approximation,” Helv. Phys. Acta, 5, 370–395 (1932).

[9] S. N. Shevchenko, S. Ashhab, and F. Nori, “Landau–Zener–Stückelberg interferometry,” Phys. Rep., 492, 1 (2010).

[10] C. Heide, T. Higuchi, H. B. Weber, and P. Hommelhoff, “Coherent Electron Trajectory Control in Graphene,” Phys. Rev. Lett., 121, 20 (2018).