QEM: Mikrowellenleiter für die Quantenelektronenmikroskopie

Motivation

Die Elektronenmikroskopie hat unser Verständnis von Welt im „sehr kleinen“ durch ihre Fähigkeit, Bilder mit atomarer Auflösung zu produzieren, revolutioniert. Aber ihre Anwendbarkeit für biologische Proben ist durch den Schaden begrenzt, den sie durch Radiolyse, Hitze und Anschlagschäden verursacht [1]. Biologische Proben überleben also nur eine bestimmte Elektronendosis, bevor sie degradieren, was die erreichbare Auflösung für einzelne Objekte auf 5-10 nm setzt [2], da die Bildinformation rauschbegrenzt ist. Eine Sub-Nanometer-Auflösung kann nur durch die Aufnahme von Tausenden von Bildern identischer Strukturen und die Verwendung eines ausgeklügelten und rechenintensiven Rekonstruktionsalgorithmus zur Erzeugung der 3-D-Struktur erreicht werden. Bilder mit atomarer Auflösung von einzelnen, isolierten biologischen Proben mit vernachlässigbarer Beschädigung der Probe sind mit der heutigen Elektronenmikroskopie nicht möglich. Die Implementierung von Messtechniken, die auf dem quantenmechanischen Phänomen der „interaktionsfreien Messung“ basieren, könnte diese Einschränkung jedoch durch die Reduzierung des Schadens überwinden und zur Entwicklung eines neuen Instruments führen: Das Quantenelektronenmikroskop (QEM) [3,4].

Interaktionsfreie Messung

Die interaktionsfreie Messung (IFM) basiert auf der Idee, dass die ein undurchsichtiges Objekt durch die Detektion eines Teilchens (z.B. Photon oder Elektron) beobachtet werden kann, das nicht im klassischen Sinne mit diesem Objekt interagiert hat [5,6]. Dieses Konzept kann mit einem Mach-Zehnder-Interferometer beschrieben werden, wie in der folgenden Abbildung dargestellt: Ein vollständig undurchsichtiges Objekt, das in einem Arm des Interferometers platziert ist, zerstört die Interferenz am Kombinationselement, was zu einer möglichen Detektion eines Teilchens am Ausgang des Interferometers in Detektor 2 führt. In diesem Fall weiß man, dass das Partikel sich entlang des unteren Strahlweges bewegt hat, wodurch ein Ereignis am Detektor 2 eintrat. Da Detektor 2 nie ein Elektron detektiert, wenn sich kein Objekt im oberen Strahlengang befindet, wurde die Anwesenheit des Objekts detektiert, obwohl es keine (klassische) Interaktion zwischen dem Objekt und dem detektierten Partikel gab. Dennoch besteht bei diesem einfachen Mach-Zehnder-Interferometer nach wie vor eine hohe Wahrscheinlichkeit, dass der Partikel am undurchsichtigen Objekt verloren geht (was zu einer Beschädigung des Objekts führen kann). Diese Technik wurde jedoch konzeptionell auf Erfolgswahrscheinlichkeiten erweitert, die beliebig nahe an 1 liegen, indem ein Ansatz analog zu einer diskreten Form des Quanten-Zero-Effekts [7] verwendet wird.

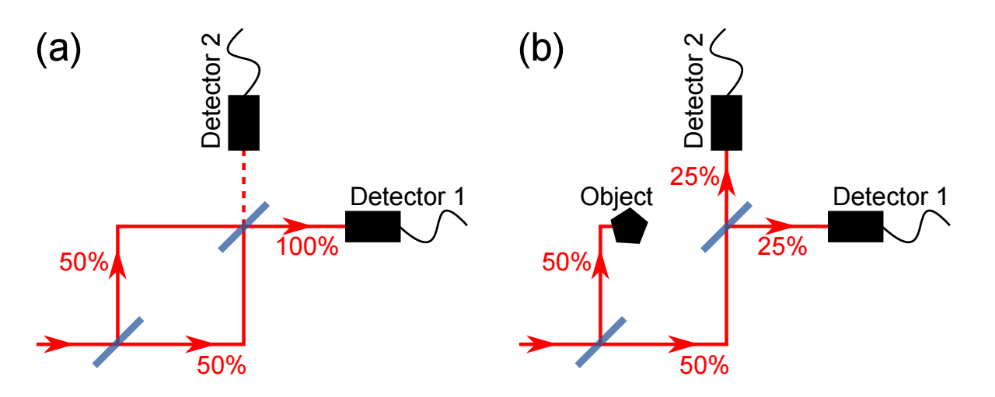
Eine interaktionsfreie Messung auf Basis eines Mach-Zehnder-Interferometers.
(a) Ein einfallendes Teilchen (Photon/Elektron) tritt von links in das Interferometer ein und wird durch einen 50/50-Strahlteiler in eine Überlagerung von zwei Wellenpaketen gespalten. Die beiden Wellenpakete durchlaufen dann die beiden Arme des Interferometers, bevor sie in einen zweiten 50/50-Strahlteiler eintreten. Die Interferometergeometrie ist so angeordnet, dass ein Teilchen aufgrund von dekonstruktiver Interferenz nie am Detektor 2 erfasst wird, sondern immer nur an Detektor 1.
(b) Wenn ein Objekt in den Weg des oberen Armes des Interferometers gebracht wird, wird eine dekonstruktive Interferenz der Zweiwellenpakete verhindert, und ein Partikel kann nun auch mit Detektor 2 detektiert werden. In diesem Fall wurde die Anwesenheit des Objekts durch Detektion eines Partikels bestimmt, das nicht mit dem Objekt (im klassischen Sinne) interagiert hat.

IFM mit hoher Erfolgswahrscheinlichkeit

Der Ansatz basiert auf der Erhöhung der Reflektivität des Strahlteilers, wodurch die Intensität des auf die betreffende Probe gerichteten Strahls reduziert wird, während das System erweitert wird, um die Probe innerhalb einer einzigen Messung mehrfach abzufragen. Ein Resonator könnte verwendet werden, um die kohärente Entwicklung der Intensitätsübertragung zwischen Proben- und Referenzstrahl zu ermöglichen, um höhere Nachweiswahrscheinlichkeiten zu erreichen und gleichzeitig die Intensität an der Probe zu reduzieren. Diese höheren Nachweiswahrscheinlichkeiten wurden experimentell für Photonen [7-9] nachgewiesen und anschließend in ein Abbildungssystem [10] implementiert. Diese fortgeschrittene IFM-Technik hat eine Erfolgswahrscheinlichkeit von 1, was bedeutet, dass ein einzelnes erfasstes Photon ausreicht, um die Anwesenheit eines Objekts im Strahlengang zu bestimmen, ohne dass das Photon vom Objekt absorbiert werden kann. Ein teilweise absorbierendes Objekt würde zu einer geringeren Erfolgswahrscheinlichkeit [11] führen, was den Nutzen des IFM-Ansatzes verringert. IFM wurde bisher noch nicht für Elektronen gezeigt, obwohl dessen Potential, den Schaden am Objekt bei der Messung zu reduzieren, gerade für die Elektronenmikroskopie von immenser Bedeutung sein könnte, da hier, wie weiter oben erläutert, die maximal erlaubte Elektronendosis der limitierende Faktor für die Auflösung ist.

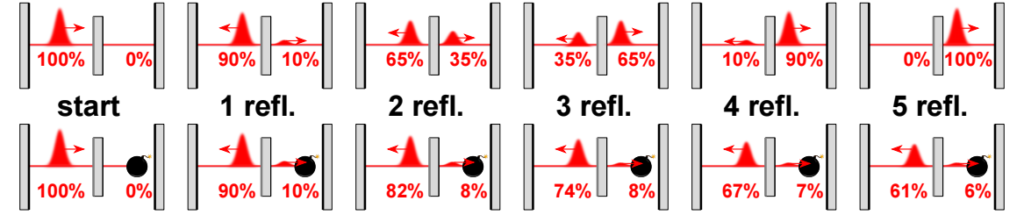
Beispiel einer interaktionsfreien Messung mit einer Erfolgswahrscheinlichkeit von ∼0.61, unter Verwendung einer hochempfindlichen Bombe als Beispielobjekt (wenn das Photon/Elektron die Bombe trifft, kommt es zur Explosion). Zwei Resonatoren sind über einen Strahlteiler mit einer Reflektivität von ρ ≈ 0.905 miteinander gekoppelt. Nach N = 5 Umläufen wird ein Photon/Elektron, das im linken Resonator startete, vollständig in den rechten Resonator übertragen, wenn dort kein Objekt ist. Der Transfer ist nichtlinear, da sich die Amplituden in den beiden Resonatoren am Strahlteiler kohärent aufaddieren. Wird der zweite Strahlengang durch die Bombe blockiert, kann dieser kohärente Aufbau nicht mehr auftreten und die Übertragung der Amplitude wird verlangsamt. Eine interaktionsfreie Detektion der Bombe erfolgt durch die Messung, ob sich das Photon/Elektron nach N = 5 Rundläufen im linken oder rechten Resonator befindet. Es gibt eine 61 prozentige Wahrscheinlichkeit die Bombe zu erkennen, ohne sie explodieren zu lassen.

QEM-Zusammenarbeit finanziert durch die Moore-Stiftung

Nachdem festgestellt wurde, dass auch mit Elektronen interaktionsfreie Messungen potentiell durchgeführt werden können [3], wurde mit Hilfe der Gordon and Betty Moore Foundation (Link: https://www.moore.org/) eine internationale Kollaboration (Link: http://www.rle.mit.edu/qem/) bestehend aus Forschungsgruppen mit Sitz in Erlangen, Delft, Boston und Stanford gegründet. Diese QEM-Kollaboration analysiert die Schwierigkeiten beim Aufbau eines interaktionsfreien Elektronenmikroskops mit atomarer Auflösung, das als Quantenelektronenmikroskop bezeichnet wird. Dieses Quantenelektronenmikroskop würde eine Reihe von einzigartigen Komponenten erfordern, die nicht in herkömmlichen Elektronenmikroskopen zu finden sind, zu denen ein kohärenter Elektronenstrahlteiler oder Zwei-Status-Koppler und eine Resonatorstruktur gehören, damit jedes Elektron die Probe mehrfach abfragen kann. Verschiedene Systemdesigns wurden vorgeschlagen [4], wir arbeitet im Speziellen an der Verwendung von On-Chip-Spiegeln als Resonanzstrukturen und an der Entwicklung eines Zwei-Zustands-Kopplers basierend auf den Pseudopotenzialen, die durch das Anlegen von Mikrowellenspannungen an entsprechend designten Elektrodenstrukturen entstehen.

Mikrowellenleiter für Elektronen

Das Grundprinzip der Mikrowellen-Elektronenleiter basiert auf dem der linearen Paul-Falle. Paul-Fallen ermöglichen das Fangen von geladenen Teilchen in einem reinen, elektrischen Wechselfeld. Feldoszillationen, die im Vergleich zur Bewegung des einzufangenden Teilchens schnell sind, führen zu einer harmonischen Rückstellkraft, die über die Zeit gemittelt wird. Die Rückstellkraft beschleunigt das Partikel immer auf ein Minimum des Feldes und ermöglicht so einen stabilen Einschluss. Da das Ladungsmassenverhältnis für Elektronen im Vergleich zu Ionen sehr hoch ist, waren Paul-Fallen bis vor kurzem auf Ionen beschränkt. Das Einfangen von Elektronen erfordert daher hohe Frequenzen für die Änderung der Polarität des elektrischen Feldes. Typische Werte für diese Frequenzen liegen im Mikrowellenbereich zwischen 1 GHz und 10 GHz. Elektronen mit einer Energie von 1 bis 10 eV werden an einem Ende des Leiters eingespeist und von den gekrümmten Elektroden in einem Winkel von 30° abgelenkt (wie in der folgenden Abbildung dargestellt). Aus diesem Grund können die geführten Elektronen räumlich von den ungeführten auf dem Detektor getrennt werden. Damit konnten wir zeigen, dass Paul-Fallen auch für Elektronen funktionieren und dass das Führen von Elektronen in zwei Dimensionen möglich ist [12,13]. Das sorgfältige Elektrodendesign und die Einstellung der Mikrowellenparameter ermöglichen eine präzise Steuerung der Felder und damit der Bewegung der geführten Elektronen. Mit einer anderen Elektrodengeometrie konnten wir ein neues elektrooptisches Instrument entwickeln: Der Mikrowellen-Elektronenstrahlteiler [14].

Elektronen folgen dem gekrümmten Mikrowellenleiter, wenn das Mikrowellenpotential eingeschaltet ist. [9]

Mikrowellen-Elektronenstrahlteiler

In unserer jüngsten Veröffentlichung [15] zeigen wir, dass wir einen Elektronenstrahl mit viel höherer Energie als bisher möglich durch eine zweischichtige Mikrowellenstruktur in zwei Strahlen teilen können. Das Funktionsprinzip dieses Elektronenstrahlteilers basiert darauf, dass die Bewegung geladener Teilchen in einem reinen elektrischen Wechselfeld auch als die Bewegung in einem effektiven Potential für vergleichsweise hohe Frequenzen beschrieben werden kann. Der Elektronenstrahl wird aufgespalten, indem das querverlaufende pseudopotenzielle Minimum, in das die Elektronen eingespeist werden, entlang der Struktur in zwei Minima aufgeteilt wird (siehe Abbildung unten). Die Elektronen folgen der Entwicklung des Pseudopotentials und werden in zwei Elektronenstrahlen aufgespalten. Die einlagigen Vorgängerstrukturen arbeiteten für Elektronenenergien von bis zu 4 eV [14], die hier durch die Verwendung von zwei aufeinander ausgerichteten Mikrowellensubstraten auf 200 eV verbessert wurde. Die Verbesserung um fast zwei Größenordnungen lässt sich durch die unterschiedliche Geometrie erklären, da die zweilagigen Strukturen viel größere geometrische Faktoren für die Berechnung der Fallenfrequenz und der Pseudopotentialtiefe aufweisen als die entsprechenden einlagigen Strukturen, was die Führung und Aufteilung eines viel energiereicheren Elektronenstrahls ermöglicht.

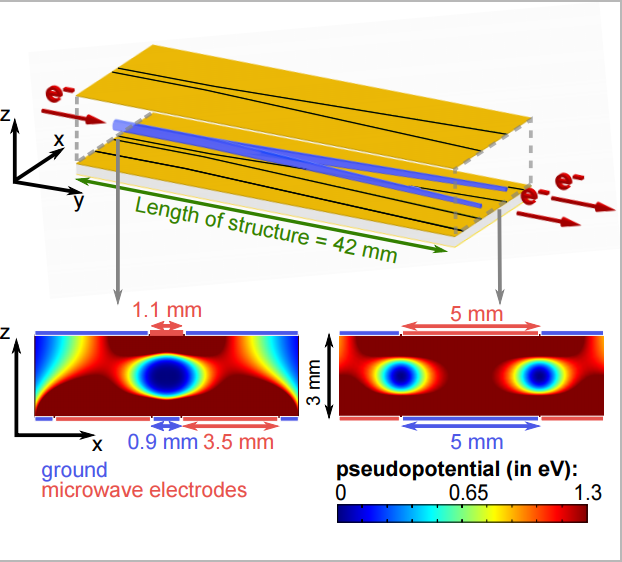
Elektrodenanordnung des zweiseitigen Mikrowellenstrahlteilers für Elektronen und Simulationsergebnisse des Pseudopotentials. Die isopotentielle Oberfläche des Pseudopotentials wird als transparent blaue Region dargestellt. Der Elektronenstrahl wird in die Mitte zwischen den Chips in y-Richtung aufgeteilt und mit zunehmender Dicke der zentralen Mikrowellenelektrode quer in zwei Strahlen aufgeteilt. [12]

Ausblick: Mikrowellen-Elektronen-Interferometer und Implementierung in einem REM

Mit zukünftigen Experimenten wollen wir die adiabatische Aufspaltung eines Elektronenstrahls zeigen, bei dem Elektronen mit einem beugungslimitierten Elektronenstrahl direkt in den Grundzustand des Pseudopotentials eingespeist werden. Im adiabatischen Limit breitet sich ein Elektronenwellenpaket entlang des Pseudopotentials aus und verbleibt im Quantengrundzustand entlang der Struktur. Überlagerung der beiden resultierenden geführten und getrennten Elektronenstrahlen an einem entfernten Detektor würde zu Interferenzstreifen führen. Ein solches mikrowellenchipbasiertes Elektroneninterferometer würde neue quantenoptische Experimente ermöglichen und könnte als Amplitudenstrahlteiler für das nicht-invasive Quantenelektronenmikroskopiekonzept verwendet werden.

Wir planen, einen solchen kohärenten Strahlteiler in ein Rasterelektronenmikroskop (REM) zu integrieren, um ein Quantenelektronenmikroskop zu realisieren (wie in der folgenden Abbildung dargestellt): Der Mikrowellenstrahlteiler wird mit einem On-Chip-Spiegel kombiniert, um das Elektron zwischen Referenz- und Probenstrahl zu übertragen.

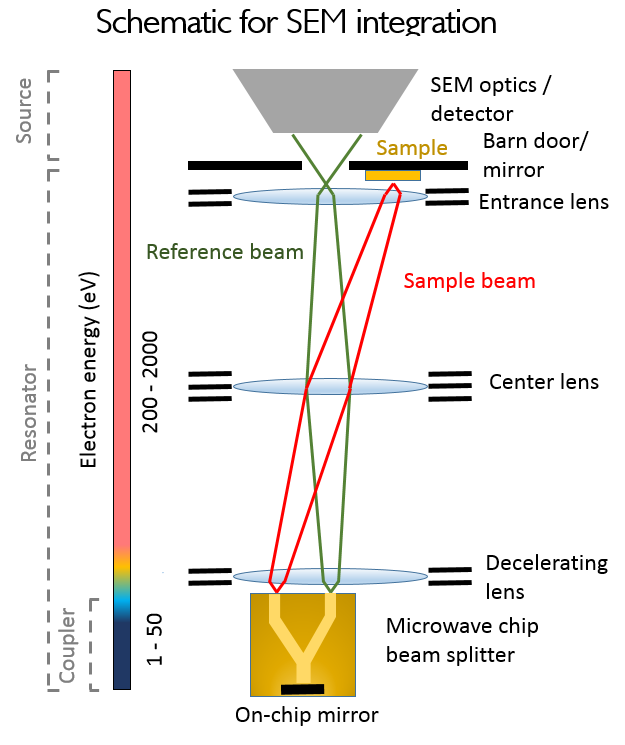
Ein Elektron wird in den Referenzstrahl injiziert. Das „Scheunentor“ (ein elektrostatischer Spiegel, der kontrolliert an- und ausgeschaltet werden kann) fängt das Elektron für eine bestimmte Anzahl von Umläufe ein, bei denen ein Teil der Amplitude der Wellenfunktion des Elektrons durch den Mikrowellenstrahlteiler in Abhängigkeit von der Opazität der Probe an der Stelle, an der der Probenstrahl fokussiert wird, in den Probenstrahl übertragen wird.

[1] D.B. Williams and C.B. Carter Transmission Electron Microscopy: A Textbook for Materials Science (2nd ed.), Springer, New York (2009)

[2] C.A. Diebolder, A.J. Koster and R.I. Koning, J. Microsc., 248 (2012), pp. 1-5

[3] Putnam, W. P., Yanik, M. F. Noninvasive electron microscopy with interaction-free quantum measurements. Phys. Rev. A 80, 040902(R) (2009).

[4] Kruit, Pieter, et al. „Designs for a quantum electron microscope.“ Ultramicroscopy 164 (2016): 31-45.

[5] Elitzur, A. C., Vaidman, L. Quantum mechanical interaction-free measurements. Foundations of Physics 23, 987–997 (1993)

[6] L. Vaidman, Found. Phys., 33 (2003), pp. 491-510

[7] Kwiat, P., Weinfurter, H., Herzog, T., Zeilinger, A., Kasevich, M. A. Interaction-free measurement. Physical Review Letters 74, 4763–4766 (1995)

[8] T. Tsegaye, E. Goobar, A. Karlsson, G. Björk, M. Loh and K. Lim, Phys. Rev. A, 57 (1998), pp. 3987-3990

[9] J.-S. Jang, Phys. Rev. A, 59 (1999), pp. 2322-2329

[10] White, Andrew G., et al. „“Interaction-free” imaging.“ Physical Review A 58.1 (1998): 605.

[11] S. Thomas, C. Kohstall, P. Kruit and P. Hommelhoff, Phys. Rev. A, 90 (2014), p. 053840

[12] Hoffrogge, Johannes; Fröhlich, Roman; Kasevich, Mark A.; Hommelhoff, Peter; Microwave guiding of electrons on a chip. Phys. Rev. Lett. 106, 193001 (2011).

[13] Hoffrogge, Johannes; Hommelhoff, Peter; Planar microwave structures for electron guiding. New J. Phys. 13, 095012 (2011).

[14] J. Hammer, S. Thomas, P. Weber, and P. Hommelhoff, “Microwave chip-based beam splitter for low-energy guided electrons,” Physical Review Letters 114, 254801 (2015).

[15] Zimmermann, R., et al. „Beam splitting of low-energy guided electrons with a two-sided microwave chip.“ Applied Physics Letters 115.10 (2019): 104103.